Diskreetse aja jaoks
On kaks kogust, mida peaksite olema ettevaatlik ja mitte segama.
- Üks on nende inimeste arv , kes teatud ajavahemiku jooksul surevad: $ d_x = N_x - N_ {x + 1} $.
- Üks on murdosa nende vahel, kes on antud intervalli alguses elus ja kes selle intervalli jooksul surevad: $ q_x = \ frac {d_x} {N_x} $
($ N_x $ on ellujäänute arv vanuses $ x $.)
Kui tavaline proovitükk on konstantne, väheneb ellujäänute arv lineaarselt; kui $ q_x $ on konstantne, väheneb ellujäämine geomeetriliselt. Kui graafikul semilog on konstant, näeb see geomeetriline langus välja sirgjoonena. See on minu teada peamine põhjus, miks isegi semiloogi proovitükke kasutada; see muudab geomeetrilise vähenemise hõlpsasti äratuntavaks. $ d_x $ nimetatakse mõnikord suremusmääraks ja $ q_x $ mõnikord suremuse määraks .
(Minu arvates on see kasutus hooletu; need pole hinnad, vaid lihtsalt numbrid. Võrdle: vahet on 10 miili tunnis läbimisel ja kell 10 miili tunnis .)
$ q_x $ võib mõelda ka kui tõenäosuse hindamist, et keegi, kes on $ x $, sureb enne $ (x + 1) $. Seetõttu nimetatakse seda mõnikord ka "surma vanusepõhiseks tõenäosuseks" . Pange tähele, et see on piiratud vahemikus 0 kuni 1.
(Tõenäosused ei tohi olla väiksemad kui 0 või suuremad kui 1; ja murduv murd peab asuma kusagil "ükski neist" ja "kõik" vahel neid "!)
Siin on näide ellujäämiskõverast, tavalisel joonisel tegin konstantse $ q_x = 0,1 $.
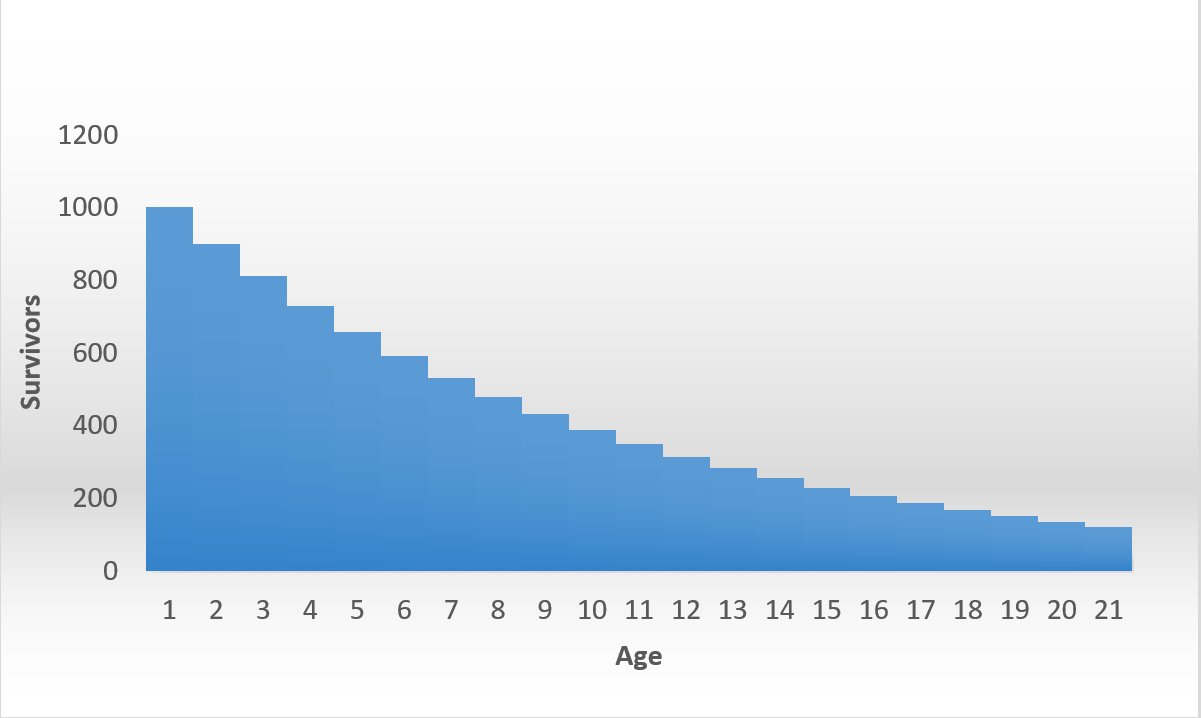
Teie küsimusele vastamiseks peaks sellest piisama. Kuid täielikkuse nimel ...
Pideva aja jaoks
Kurtsin, et nimetasin suremuseks $ d_x $. Seda seetõttu, et tariifide ühik on $ aja ^ {- 1} $ ("... sekundis ", "... tunnis " jne) Muidugi , jagades $ d_x $ intervalli pikkusega , saate keskmise intervalli suremuse. Ja
- ellujäämiskõvera kalle (korrutatuna -1-ga; soovime negatiivse kasvu määra asemel positiivset langusmäära) annab teile hetkeline suremus vanuses $ x $: $ -N ^ {'} _ {x} $.
(Et hetkemäärad oleksid kasulikud, peame ellujäämiskõvera "siluma", selle asemel, et lasta sellel astmelist kõverat. Kui see oleks astmeline, oleks kalle lihtsalt alati ole horisontaalne või vertikaalne.)
See viib meid teise suuruse juurde: " suremuse jõud ":
- hetkeline, eakohane , suremus inimese kohta ; või suremus vanuses $ x $ jagatuna kohordi suurusega vanuses $ x $: $ \ mu_x = - \ frac {N ^ {'} _ {x}} {N_x} $
Illustreerimaks, kas suremus vanuses $ x $ on " 60 surma minutis " ja kui see on kohe, kui seal on 60 inimest, on inimese kohta suremuse määr " 1 surm inimese kohta minutis ". Kuna ajaühiku valik on meelevaldne, on see sama, kui öelda " 60 surma inimese kohta tunnis " või " 525600 surma inimese kohta aastas ".
Suremuse jõud ei ole mõistlik (inimese kohta on suremus? - aga kõik surevad ainult üks kord!), kuid valem on sidus. "Ühe elaniku määra" mõte on võimaldada võrrelda erineva suurusega kohorde või sama kohordi erinevas vanuses, kui see oli suurem vs väiksem, ja nii edasi; üldiselt on mõte see, et suremusel on midagi pistmist liikmete arvuga, aga ka see, mis on seotud iga liikme olukorraga, ja $ \ mu_x $ üritab viimast saavutada. Seda saab visualiseerida kui ellujäämiskõvera kalle (korrutatuna -1-ga, et see oleks positiivne), jagatuna ellujäämiskõvera kõrgusega .
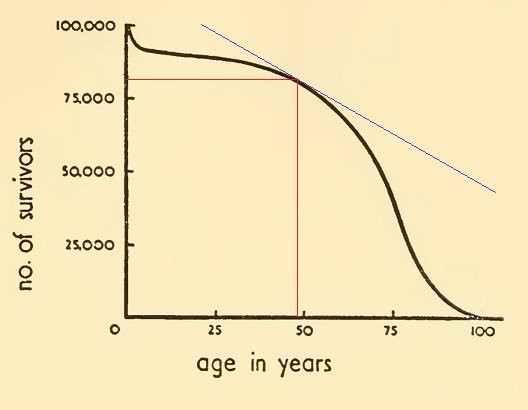
Nende kahe suuruse ja kahe diskreetse aja jaoks määratletud koguse vahel on sarnasus. Kui $ -N ^ {'} _ {x} $ on konstantne, siis on ka $ d_x $; ja kui $ \ mu_x $ on konstantne, siis on ka $ q_x $. Ja veel kord: kui tavalisel joonisel on $ -N ^ {'} _ {x} $ konstantne, väheneb ellujäämine lineaarselt; ja kui $ \ mu_x $ on konstantne, väheneb ellujäämine eksponentsiaalselt.
Kuid need on erinevad. See on mõõde $ time ^ {- 1} $ ja asjaolu, et ajaühikud on omavahel asendatavad.
Kui inimesi on ainult 60, pole see ilmselgelt võimalik üle 60 järgmise aasta jooksul surevad inimesed $ (0 \ le d_x \ le 60) $; ja pole võimalik, et surev murd oleks suurem kui "kõik need" $ (0 \ le q_x \ le 1) $.
Kuid oletame, et surma hetkeks on surma määr 60 surma tunnis . See on sama asi, kui öelda, et see on " 1 surm minutis " või " 525600 surma aastas ". Pole mingit vihjet, et nii paljud inimesed tegelikult surevad, sest pole aimugi, et kogu aasta jooksul seda kurssi hoitakse . Kui seda konkreetset suremust hoitaks võimalikult kaua konstantsena, siis oleks kohort kõik täpselt tunni aja pärast surnud ja seejärel tabaks see määr 0. Hetke suremus võib olla nii kõrge kui soovite; see lihtsalt ei saa püsida kõrgel igavesti.
(Kui suremuse määra " 60 surma tunnis " mõõdetakse hetkel, kui 60 inimest, siis on inimese kohta suremuse määr " 1 surm inimese kohta tunnis " - või samaväärselt " $ \ frac {1} {60} ^ {th} $ surm inimese kohta tunnis "või" 8760 surmajuhtumit inimese kohta aastas ".)
Kuigi absoluutne suremus ei saa jääda igaveseks kõrgeks, inimese kohta suremus ($ \ mu_x $) saab . Nii juhtub näiteks konstantse $ \ mu_x $ ajal (eksponentsiaalselt vähenev $ N_x $). Põhjus, miks see pole paradoksaalne, on see, et kalle ($ -N ^ {'} _ {x} $; lugeja) väheneb pidevalt; lihtsalt nii on ka kõrgus ($ N_x $; nimetaja).
Suremuse jõudu $ \ mu_x $ on ka mõnikord nimetatud kui " suremuse määr ". Kahetsusväärne keelekasutus on kahetsusväärne. See on ka eriti töökindluse inseneriteaduses tuntud kui "ohumäär".
Muide
$ q_x $ ja $ \ mu_x $ on gerontoloogias (mida ma kõige paremini tunnen) sageli segamini aetud. Kuid nad pole ühesugused. Esimene hindab tõenäosust ja jääb vahemikku 0 kuni 1. Teine pole mitte tõenäosus ja sellel puudub ülemine piir.
Üks viis, kuidas neid on segatud, on " Gompertzi võrrand ".
II tüüpi ellujäämise kõver on see, mis väheneb eksponentsiaalselt. Sel juhul on nii $ q_x $ kui ka $ \ mu_x $ konstantsed. Nimetaksime sellist liiki "vananemata" või "vananemata": teie vanus ei oma haavatavusele vahet.
Kuid paljud liigid vananevad.
^ {Gx} $
Või logaritmilises vormis: $ ln (\ mu_x) = ln (\ mu_0) + Gx $ (kus $ \ mu_0 $ on "esialgne suremus" ja $ G $ on eksponentsiaalne "Gompertzi parameeter". Logaritmilisel kujul on lõikepunktiks $ ln (\ mu_0) $ ja $ G $ on kalle.)
Kas $ \ mu_x $ järgib sellist seadust lõputult või mitte, on empiiriline küsimus. (Tegelikult vaieldakse selle üle, kas see hilisemas elus aeglustub ja kui jah, siis miks.) Kuid pange tähele, et $ q_x $ ei saanud võimalik kasvada igavesti eksponentsiaalselt, kuna $ q_x $ ei saanud võimalik ületavad kunagi 1. Ja ometi on segaduse tõttu Gompertzi võrrandit esitletud ja arutatud viimasel ajal sageli $ q_x $ osas.
Edasine lugemine
Minu teada on kirjandusest (nii professionaalsest kui ka pedagoogilisest) nii intuitiivse kui ka täpse ravi puudumisel väga puudulik!
Peter Medawari teos "Senesentsuse määratlus ja mõõtmine" (1. peatükk The CIBA Foundation Colloquia on Aging, Vol. 1 ) on ilmselt endiselt parim sissejuhatus põhjendusele, miks me hoolime ellujäämise kõveratest ja suremusest biogerontoloogia vaatenurgast. Medawar annab $ \ mu_x $ -le õige definitsiooni ja valemi (kuigi ta ei rõhuta selle eristamist $ q_x $ -st; tõepoolest, ta ei maini üldse $ q_x $).
Teenuste $ q_x $ ja $ \ mu_x $ eristamist käsitletakse nii Gavrilovi ja Gavrilova teoses The Biology of Life Span: A Quantitative Approach kui ka mõnes nende artiklis. Nad esitavad õige foorumi $ \ mu_x $ jaoks, kuid ei püüa seda tegelikult seletada.